算法实现部分依据《基于决策树技术在高考成绩的分析研究》论文来对文中算法进行实现,运用决策树分类技术对高考理科生考试的六个科目数据进行更深层次的有效分析处理,从中发现各科成绩对总成绩的影响,提取出由决策树生成的分类规则,对高中教育具有一定的指导意义和实践价值。
1. 数据获取
算法实现采用某高三期末考试成绩表作为研究对象,数据如下: 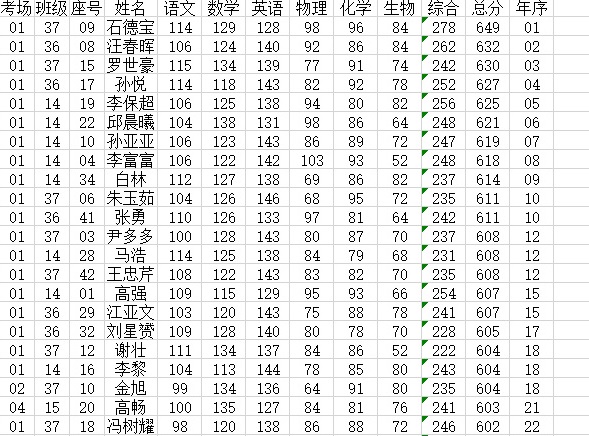
2. 数据处理
2.1 获得干净数据
利用pandas处理数据,将成绩缺失的记录进行删除,将姓名、班级、年序、综合删除,由考场号加座号构成考号。
代码如下:

结果:

2.2 对数据进行离散化处理
由于决策树的 ID3 算法只能处理离散化的数据,所以要对成绩数据进行离散化的处理。高考考试的试卷总分数是750分,通常人们认为高考的本科线为各科及格分数的总和,因此根据总分是否大于450分进行设置,将“总分”字段按照大于等于450分的为“PASS”,否则为“NOPASS”。语文、数学和英语满分为 150分,按照 110、90划分为三个层次,分别记为“A”、“B”、“C”三个等级。物理、化学、生物满分为100分,按照80、60划分为三个层次,分别记为“A”、“B”、“C”三个等级。
代码如下:

结果:

3. 构建决策树
决策树模型是最常用的一种数据挖掘方法。它可以直接表现数据的特点,有利于理解,具有良好的分类预测能力,并能促进提取决策规则。ID3算法属于一种自顶向下、分而治之的递归构造决策树的贪心算法。其优点是在测试属性的选择上,利用了信息增益的概念,描述简单,构造的决策树平均深度较小,分类速度快,学习能力强,适合于大规模的数据处理。ID3算法在决策树构建的过程中,最重要的就是根结点的选择。ID3算法首先找出具有最大信息增益的属性作为当前的分裂结点。然后把当前样本分成多个子集,每个子集又选择最大信息增益的属性划分,一直进行到所有子集仅包含同一类型的数据为止。
3.1 计算分类属性的期望信息
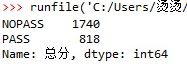
已知nopass人数为1740人,pass人数为818人。因此分类属性的期望信息为:

3.2 计算出各科属性的信息量
以语文为例:

如上图可以看出:“语文”属性取值分别为“A”、“B”、“C”。其中,58 个“A”样本中“PASS”的有 46 个,“NO⁃PASS”的有 12 个;1180 个“B”样本中“PASS”有 368 个,“NOPASS”有 812个;1320个值为“C”样本中“PASS”有404个,“NOPASS”有 916个。通过以下公式计算得到“语文”的信息增益:

然后将各门科目的信息增益率计算出来,进行比较,选择信息增益最大的值来作为决策树的根节点,然后层层来建立我们的决策树。
{ 这是手动算出来的,算了半条老命…接下来编写代码验证结果的正确性 }
首先,先对数据进行一些处理,得到计算信息增益所需要的数据:
df2=pd.DataFrame(columns=['all','pass','nopass'])
df2['all']=df[line].value_counts()
df2['pass']=df[df["总分"]=='PASS'][line].value_counts()
df2['nopass']=df[df["总分"]=='NOPASS'][line].value_counts()

编写信息增益函数代码:
def Gainvalue(subdata,HD,count):#计算信息增益
I=[]
returnvalue=[]
E=0
for index, row in subdata.iterrows():
value=[]
for col_name in subdata.columns:
value.append(row[col_name])
I.append(CountHDA(value))
for i in range(len(subdata)):
E=E+(subdata['all'][i]/count)*I[i]
gain=HD-E
returnvalue.append(gain)
returnvalue.append(I)
return returnvalue
得到结果:

可见,与上面计算的结果相同。
然后设置函数,分别计算各个学科的信息增益值:
def Getsubdata(subject,HD,df): #获得各个科目的统计数据
allvalue=[]
df3=pd.DataFrame(columns=['all','pass','nopass']) #定义d3 dataframe
for line in subject:
df2=pd.DataFrame(columns=['all','pass','nopass'])
df2['all']=df[line].value_counts()
df2['pass']=df[df["总分"]=='PASS'][line].value_counts()
df2['nopass']=df[df["总分"]=='NOPASS'][line].value_counts()
df3=df3.append(df2) #保存未被处理为1的nan值
df2.fillna(1, inplace=True) #将nan值改成1
allvalue.append(Gainvalue(df2,HD,2558))
此处出现生物学科nopass中为空的情况,本来想将其替换为0,但是在计算经验熵时分母为0会爆错误,我就设置了1,这样不会导致错误,也对结果影响小。
最后得到各个科目的信息熵与信息增益值:

这里可见,化学科目信息增益值最大,为0.268408006259。而论文中测量出来的结果数学信息增益值最大。因为这里测量的理科外加上数据不同,并且如果这次化学考试出的题偏怪偏难,也会导致这样的结果。
3.3 基于决策树的科目重要性排序
设置六次循环,在基于上一门重要科目之上再计算其他科目的信息增益值,再使得此时最大信息增益值为下一门重要科目。
计算所有科目的重要性的代码如下:

结果为:

但这只是基于前一门科目计算信息增益值,而决策树是针对所有分支,所以这只是一个初步的预测。接下来是对获得最起决定性作用的科目分ABC类进行计算:
首先对Getsubdata()进行修改:
def Getsubdata(subject,HD,df): #获得各个科目的统计数据
allvalue=[]
df3=pd.DataFrame(columns=['all','pass','nopass']) #定义d3 dataframe
for line in subject:
df2=pd.DataFrame(columns=['all','pass','nopass'])
df2['all']=df[line].value_counts()
df2['pass']=df[df["总分"]=='PASS'][line].value_counts()
df2['nopass']=df[df["总分"]=='NOPASS'][line].value_counts()
df3=df3.append(df2) #保存未被处理为1的nan值
df2.fillna(1, inplace=True) #将nan值改成1
allvalue.append(Gainvalue(df2,HD,2558))
maxindex,maxE=Getmax(allvalue) #获得gain最大的index和所有经验熵值
gettotalvalue(maxindex,df3[3*maxindex:3*(maxindex+1)],maxE)#最大的index,获得gain最大的ABC各个统计值,最大的E
Getmax()函数用来获得信息增益最大的科目在subject的list中的index以及各个条件熵的值。
def Getmax(allvalue):
maxindex=allvalue.index(max(allvalue))
maxE=allvalue[allvalue.index(max(allvalue))][1]
return maxindex,maxE
然后编写gettotalvalue(),用于各个分支进行计算(ABC类):
def gettotalvalue(maxindex,maxvalue,maxE):#判断是否还需要继续取值
maxsubject=subject[maxindex]
i=0
# print(maxvalue)
maxvalue=maxvalue.dropna(axis = 1, how ='any')
for index, row in maxvalue.iterrows(): # 获取每行的index、row
Getnextbranch(maxE[i],maxsubject,index,subject)
#分支的经验熵值(作为下一轮计算)、获得gain最大的科目,等级(ABC),全部科目,数据,数据总数
i=i+1
编写得到决策树第二层重要性科目的函数Getnextbranch():
def Getnextbranch(HD,maxsubject,level,subject):#计算下一支的取值
secondvalue=[]
df3=pd.DataFrame(columns=['all','pass','nopass']) #定义d3 dataframe
for line in subject: #下一层的科目进行统计
df4=pd.DataFrame(columns=['all','pass','nopass'])
df4['all']=df[df[maxsubject]==level][line].value_counts()
df4['pass']=df[df[maxsubject]==level][df["总分"]=='PASS'][line].value_counts()
df4['nopass']=df[df[maxsubject]==level][df["总分"]=='NOPASS'][line].value_counts()
df3=df3.append(df4) #保存未被处理为1的nan值
df4.fillna(1, inplace=True) #将nan值改成1
if line!=maxsubject:
secondvalue.append(Gainvalue(df4,HD,len(df[df[maxsubject]==level])))
maxindex,maxE=Getmax(secondvalue)
secondsubject=subject[maxindex]
levels=['A','B','C']
flag=0
for secondlevel in levels:
Getthirdbranch(maxE[flag],subject,maxsubject,secondsubject,level,secondlevel)
flag=flag+1
其实跟上面差不多,这里只是加上第一层重要性科目(这里为化学)、等级这两个约束条件将数据进行重新分类统计,然后再用特定等级的化学成绩的经验熵来进行第二层进行计算。得到最大的信息增益对应的科目。
计算结果如图:

可以看出化学为B、C时英语最为重要,而化学为A时物理更重要。
得到第二层后,就来得到第三层的决策树(因为科目少,到后面影响很少,就设置三层决策树了)
第三层代码如下:
def Getthirdbranch(maxE,subject,maxsubject,secondsubject,maxlevel,secondlevel):#计算第三支的取值
thirdvalue=[]
df5=pd.DataFrame(columns=['all','pass','nopass']) #定义d3 dataframe
# print(subject)
for line in subject: #下一层的科目进行统计
df6=pd.DataFrame(columns=['all','pass','nopass'])
df6['all']=df[df[maxsubject]==maxlevel][df[secondsubject]==secondlevel][line].value_counts()
df6['pass']=df[df[maxsubject]==maxlevel][df[secondsubject]==secondlevel][df["总分"]=='PASS'][line].value_counts()
df6['nopass']=df[df[maxsubject]==maxlevel][df[secondsubject]==secondlevel][df["总分"]=='NOPASS'][line].value_counts()
df5=df5.append(df6) #保存未被处理为1的nan值
df6.fillna(1, inplace=True) #将nan值改成1
if line!=maxsubject:
thirdvalue.append(Gainvalue(df6,HD,len(df[df[maxsubject]==maxlevel][df[secondsubject]==secondlevel])))
maxindex,maxE=Getmax(thirdvalue)
print(maxsubject,maxlevel,secondsubject,secondlevel,subject[maxindex])
和一二层类似,这里计算数据再添加决策树第二层的约束,比如求化学C英语A下的最重要的科目时,就需要在化学C英语A数据下进行各个科目的数据统计。
然后计算结果为:

画出决策树如下图:

4. 基于决策树的结果分析
由上面结果可见,化学成绩为影响成绩的重要因素。据我高三经验来说,对理科生而言其实化学不会拉开太多距离,我想应该是这次化学考试出的难度较大题型偏怪所致。紧接着影响学生成绩的是英语、物理。这个我非常赞成,有很大一部分男生英语成绩不好而有些女生英语特别好,导致差距很大。 然后,物理科目对于很多女生而言来说,真的是非常一头雾水(比如我),所以这个影响也极大。然后就是数学和语文,其实数学相对而言应该比语文更重要,但这里只记录了三层,所以这个结果是粗略的。生物是理科最简单的一门,毋庸置疑。所以理科生要想取得好成绩应该多在化学、英语、物理上下功夫。